Asymmetric-Key Encryption and Digital Signatures in Practice

In this article, we will learn how asymmetric-key encryption and digital signatures work from a practical perspective.

In the previous article, we learned the basics of symmetric-key encryption, including how to generate keys using a password-based key derivation function called PBKDF2, how block ciphers work and how to encrypt/decrypt data with AES in ECB and CBC modes.

In this article, we will deep dive into asymmetric-key encryption and digital signatures.

Again, we will use OpenSSL to put into practice some concepts about asymmetric-key encryption. Feel free to follow along with this article and run the commands on your machine. You just need a terminal with a recent version of OpenSSL.

Let’s get started!

Asymmetric-key encryption

In asymmetric-key encryption (also called public-key encryption) we need a pair of keys, usually called public and private keys. Data encrypted with the public key can only be decrypted with the private key.

Let’s say you want to share some private information with a friend, and you want to send this information encrypted. With a symmetric-key encryption algorithm like AES, you would need your friend’s private key to encrypt the information. Securely exchanging the key is always a challenge, because if someone is able to intercept the communication, the private key could leak and the security is broken!

This problem is solved when using an asymmetric-key encryption algorithm. You just have to ask your friend to send you her public key, which is, well, public! Then you use this public key to encrypt the information. Since the generated ciphertext can only be decrypted with the corresponding private key, only your friend would be able to decrypt it.

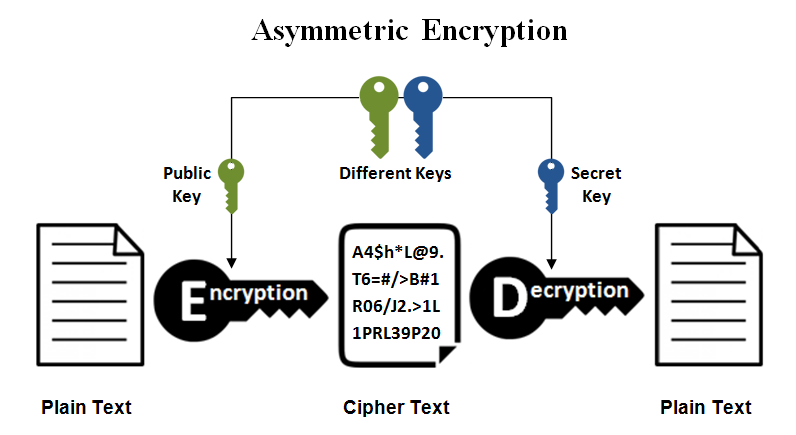
There are several asymmetric-key encryption algorithms available, including RSA and Elliptic Curve Cryptography (ECC). The most commonly used is RSA (also one of the oldest), publicly described in 1977 by Ron Rivest, Adi Shamir and Leonard Adleman (the acronym “RSA” comes from their surnames).

So let’s start our experimentation by creating the public and private keys for RSA encryption.

Generating a public/private key

RSA works with keys up to 4096 bits. The longer the key, the better, since it improves the security against brute-force attacks. Also, you can encrypt more data with a longer key (though the encryption will take more time).

In this article, let’s work with a 4096 bits key.

The private key for RSA encryption can be created with the command below:

$ openssl genrsa -out priv.key 4096

The corresponding public key can be generated by taking the private key as input:

$ openssl pkey -pubout -in priv.key -out pub.key

Both will be text files with the keys encoded, looking something like this:

$ head -3 priv.key pub.key
==> priv.key <==
-----BEGIN PRIVATE KEY-----
MIIJQwIBADANBgkqhkiG9w0BAQEFAASCCS0wggkpAgEAAoICAQDmpDOUGVAQ9mzo
UH7ocJ3GB6zwqR2YHsUssotbHtUSi8OOzNtVDMh2jlSQx7feB0dWmVxSqQyQtyDn

==> pub.key <==
-----BEGIN PUBLIC KEY-----
MIICIjANBgkqhkiG9w0BAQEFAAOCAg8AMIICCgKCAgEA5qQzlBlQEPZs6FB+6HCd
xges8KkdmB7FLLKLWx7VEovDjszbVQzIdo5UkMe33gdHVplcUqkMkLcg56mkN+J8

Now we are ready for some asymmetric-key encryption!

Encryption with RSA

Let’s encrypt a simple text file:

$ echo "The answer to Life, the Universe, and Everything is 42." > cleartext.txt

The command below will encrypt the file using the public key (-inkey pub.key -pubin), taking the input file provided by the -in option and creating an encrypted file called ciphertext.txt via the -out option:

$ openssl pkeyutl -encrypt -inkey pub.key -pubin -in cleartext.txt -out ciphertext.txt

Obs.: In older versions of OpenSSL, the subcommand rsautl can also be used as an alternative to pkeyutl.

Now let’s try to decrypt the ciphertext, but using the public key:

$ openssl pkeyutl -decrypt -inkey pub.key -in ciphertext.txt
Could not read private key from pub.key
409750C3497F0000:error:1608010C:STORE routines:ossl_store_handle_load_result:unsupported:../crypto/store/store_result.c:151:
409750C3497F0000:error:1608010C:STORE routines:ossl_store_handle_load_result:unsupported:../crypto/store/store_result.c:151:
pkeyutl: Error initializing context

Yeah, it doesn’t work because the ciphertext can only be decrypted with the private key!

So let’s try again, now with the private key:

$ openssl pkeyutl -decrypt -inkey priv.key -in ciphertext.txt
The answer to Life, the Universe, and Everything is 42.

Nice!

But can we encrypt a larger file with RSA?

Encrypting large files

Let’s create a file with 1Mb in size to test RSA encryption on larger files:

$ dd if=/dev/random of=cleartext-big.txt bs=1M count=1

Now let’s try to encrypt it:

$ openssl pkeyutl -encrypt -inkey pub.key -pubin -in cleartext-big.txt -out ciphertext-big.txt
Public Key operation error
40F78625227F0000:error:0200006E:rsa routines:ossl_rsa_padding_add_PKCS1_type_2_ex:data too large for key size:../crypto/rsa/rsa_pk1.c:129:

It doesn’t work! That is because RSA has some limitations on the size of the block to be encrypted. And the size of the block depends on the size of the key. For example, for a 4096 bits key, the block is 512 bytes minus padding.

We could break down the data into small blocks to encrypt with RSA, but that is not common. RSA is a relatively slow algorithm, and it’s not commonly used to directly encrypt large amounts of data.

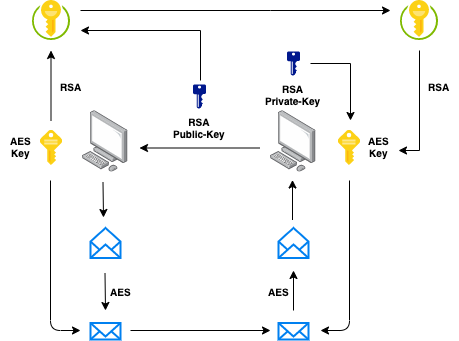
So how can we solve this problem? Easy peasy! We can combine the convenience of public-key encryption with the efficiency of symmetric-key encryption! In other words, we can use AES to encrypt the data (because is faster and more efficient) and solve the key exchange problem by encrypting the AES private key with the RSA public key. Wait, what?

Take a deep breath. Let’s see how this is done!

First, create a private key and an initialization vector for AES encryption:

$ openssl enc -pbkdf2 -aes-128-ecb -k my-secret-passphrase -P
salt=291F74776135CAF2
key=4A48195DFA143D17F44AB817C831FACF

$ echo 4A48195DFA143D17F44AB817C831FACF > key.priv

$ openssl rand -hex 16 > iv.txt

Encrypt the data with this key:

$ openssl enc -aes-128-cbc -in cleartext-big.txt -K $(cat key.priv) -iv $(cat iv.txt) -out ciphertext-big.txt

And encrypt the key the RSA’s public key:

$ openssl pkeyutl -encrypt -inkey pub.key -pubin -in key.priv -out key.priv.enc

Now we have the encrypted data, encrypted key, and initialization vector:

$ file ciphertext-big.txt key.priv.enc iv.txt
ciphertext-big.txt: data
key.priv.enc:      data
iv.txt:            ASCII text

This is what you would need to provide to the person that will decrypt the information. Only the one with the RSA’s private key will be able to decrypt it!

First, you have to decrypt the encryption key:

$ openssl pkeyutl -decrypt -inkey priv.key -in key.priv.enc -out key.priv

And use it to decrypt the data:

$ openssl enc -d -aes-128-cbc -in ciphertext-big.txt -K $(cat key.priv) -iv $(cat iv.txt) -out cleartext-big.txt

Done!

This is basically what happens when we securely exchange information over the Internet.

An asymmetric-key encryption algorithm is used to create and exchange a session key that is used in a symmetric-key encryption algorithm to encrypt the data. We have the convenience (and security) of not needing to exchange a private key and the efficiency provided by a symmetric-key encryption algorithm to encrypt the data (SSL/TLS in a nutshell).

There is one last concept we need to understand when we talk about asymmetric-key encryption, and that is called digital signatures!

Digital signatures

Encryption is about confidentiality, and we will use it to protect the information from disclosure to unauthorized parties.

But what about authenticity? What if what we want is to validate the origin of the information, making sure it’s coming from a source we trust? This is where digital signatures come in.

A digital signature is a mathematical scheme for verifying the authenticity of digital messages or documents.

Let’s say you want to send a message to a friend:

$ echo "The answer to Life, the Universe, and Everything is 42." > message.txt

But your friend needs to make sure the message is coming from you.

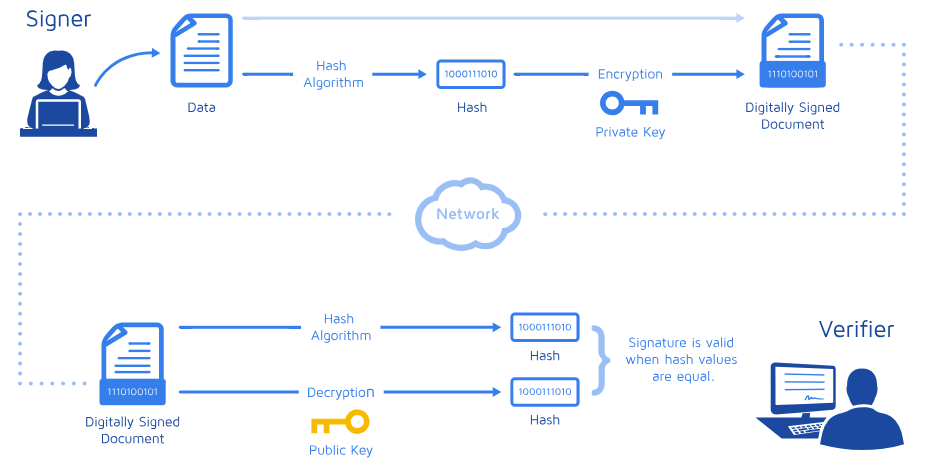
To solve this problem, you create a hash of the message and encrypt it with your RSA’s private key. A hash function is any function that can be used to map data of arbitrary size to fixed-size values. This is nice because it doesn’t matter the size of the message, the hash “represents” the message and will always have a fixed size that can be easily and quickly encrypted by an asymmetric-key encryption algorithm.

The complete operation (creating and encrypting the hash) can be done in OpenSSL with the command below:

$ openssl dgst -sha256 -sign priv.key -out message.sig message.txt

Now you have to send your friend the original message and the encrypted (signed) hash:

$ file message.txt message.sig
message.txt: ASCII text
message.sig: data

Checking the signature is the reverse operation. You take the encrypted hash, decrypt it with the public key and compare the result with the hash of the original message. If it matches, the signature is validated!

Again, this can be done in OpenSSL with just one command:

$ openssl dgst -sha256 -verify pub.key -signature message.sig message.txt
Verified OK

In addition to authentication, a digital signature ensures that data hasn’t been tampered with or changed during transmission, aka data integrity!

You can confirm this by changing the message and checking the signature again. The check will fail:

$ echo bla >> message.txt

$ openssl dgst -sha256 -verify pub.key -signature message.sig message.txt
Verification failure
4017AE10467F0000:error:02000068:rsa routines:ossl_rsa_verify:bad signature:../crypto/rsa/rsa_sign.c:430:
4017AE10467F0000:error:1C880004:Provider routines:rsa_verify:RSA lib:../providers/implementations/signature/rsa_sig.c:774:

When you have both authenticity and integrity, the legitimacy of the data (both origin and content) cannot be denied. In the security field, this is usually called non-repudiation!

Here is a summary of the digital signature process:

There is one last problem here. When someone sends you a signed message and a public key, why should you trust this public key? What if the public key and the signed message were tampered with during transmission? This is solved by certificates and a public-key infrastructure (PKI), but it’s a topic for another blog post. :-)

I hope you had some fun. Until next time!

About the author: Sergio Prado has been working with embedded systems for more than 25 years. If you want to know more about his work, please visit the About Me page or Embedded Labworks website.

Please email your comments or questions to hello at sergioprado.blog, or sign up the newsletter to receive updates.

See also

• What are random numbers and how they are managed on Linux?
• Introduction to TPM (Trusted Platform Module)
• RPMB, a secret place inside the eMMC
• Introduction to SBOM management on embedded Linux
• A hands-on approach to symmetric-key encryption